[메타코드 강의 후기] 딥러닝 Deep Learning | Regression

LEGGO약 2 분

메타코드?

메타코드는 IT 대기업 현직자 + 서울대/카이스트 AI 박사 등 검증된 강사진들로 구성되어 있으며,

현직자 특강, 커리어 멘토링, 포트폴리오, 공모전, 채용정보 등 실제 취업에 도움이 될 수 있는 양질의 컨텐츠를 제공하고 있다.

One-Hot Encoding

원-핫 인코딩(One-Hot Encoding)은 범주형 변수를 이진 벡터로 변환하는 방법이다. 각 범주형 값은 벡터 내에서 하나의 요소만이 1이고 나머지는 모두 0인 형태로 변환된다. 이는 기계 학습 모델이 범주형 변수를 처리할 수 있도록 도와준다.

예제

예를 들어, 색상이라는 범주형 변수가 있다고 가정하면 이 변수는 세 가지 값(빨강, 초록, 파랑)을 가질 수 있다.

색상
빨강
초록
파랑
빨강

이 변수를 원-핫 인코딩하면 다음과 같이 변환된다:

색상_빨강	색상_초록	색상_파랑
1	0	0
0	1	0
0	0	1
1	0	0

구현

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 데이터 생성
data = {
    '색상': ['빨강', '초록', '파랑', '빨강', '파랑', '초록'],
    '크기': [1, 2, 3, 4, 5, 6],
    '가격': [10, 15, 20, 25, 30, 35]
}

df = pd.DataFrame(data)

# 원-핫 인코딩 수행
df_encoded = pd.get_dummies(df, columns=['색상'])

# 독립 변수(X)와 종속 변수(y) 분리
X = df_encoded.drop('가격', axis=1)
y = df_encoded['가격']

# 학습 데이터와 테스트 데이터로 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')

# 회귀 계수
print('Coefficients:', model.coef_)
print('Intercept:', model.intercept_)

# 데이터프레임 출력
print(df_encoded)

Regression

Input 변수(x)를 통해 연속형 변수인 output(y, label, 종속변수)를 예측하는 모델링 기법

연속형 변수의 예측이기 때문에 예측값과 실제값의 차이를 통해 모델 성능을 평가한다.

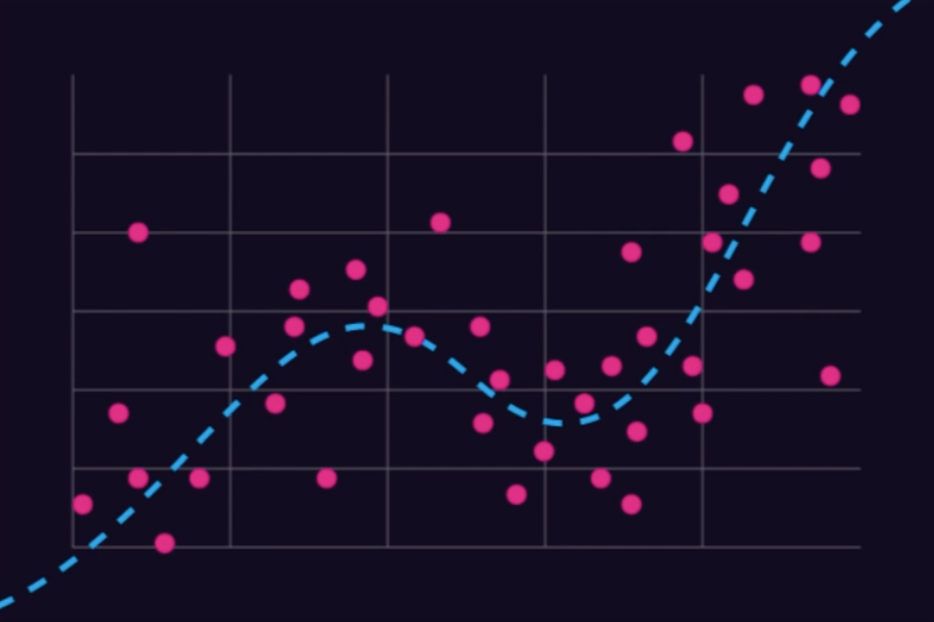
Linear Regression

정의

선형 회귀는 가장 기본적인 회귀 방법으로, 독립 변수 $X$ 와 종속 변수 $Y$ 사이의 선형 관계를 모델링한다. 목표는 주어진 데이터에 가장 잘 맞는 직선을 찾는 것이다.

수학적 모델

선형 회귀 모델은 다음과 같은 수학적 형태를 가진다: $y = \beta_0 + \beta_1 x + \epsilon$ 여기서,

$y$ : 종속 변수 (예측하고자 하는 값)
$x$ : 독립 변수 (설명 변수)
$\beta_0$ : 절편 (회귀선이 y축과 만나는 점)
$\beta_1$ : 기울기 (독립 변수 $x$ 가 1 단위 증가할 때 종속 변수 $y$ 의 변화량)
$\epsilon$ : 오차 항 (모델이 설명하지 못하는 부분)

선형 회귀의 목표는 데이터 포인트들이 있는 공간에서, 각 포인트와 회귀선 사이의 거리를 최소화하는 것이다. 이를 위해 일반적으로 최소 제곱법(Ordinary Least Squares, OLS)을 사용하여 다음 목적 함수를 최소화한다: $\min_{\beta_0, \beta_1} \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_i))^2$

가정

선형 회귀 모델은 다음과 같은 몇 가지 가정을 한다:

선형성: 독립 변수와 종속 변수 사이의 관계가 선형이어야 한다.
독립성: 관측치 간의 오차가 독립적이어야 한다.
등분산성: 모든 관측치의 오차 분산이 동일해야 한다.
정규성: 오차 항이 정규 분포를 따라야 한다.

예제

예를 들어, 어떤 회사의 광고비와 매출 간의 관계를 분석한다고 했을 때, 광고비를 독립 변수 $x$ 로, 매출을 종속 변수 $y$ 로 두고 데이터를 수집한 후, 선형 회귀를 통해 광고비가 매출에 미치는 영향을 분석할 수 있다.

구현

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 샘플 데이터 생성
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([1.2, 1.9, 3.1, 3.9, 5.1])

# 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)

# 예측
y_pred = model.predict(X)

# 시각화
plt.scatter(X, y, color='blue')  # 데이터 포인트
plt.plot(X, y_pred, color='red')  # 회귀선
plt.xlabel('X (광고비)')
plt.ylabel('y (매출)')
plt.title('선형 회귀 예제')
plt.show()

Multiple Regression

정의

다중 회귀는 여러 개의 독립 변수를 사용하여 종속 변수를 예측하는 회귀 기법이다. 이는 단순 회귀에서 독립 변수의 개수를 확장한 형태로, 독립 변수 $X$ 들이 종속 변수 $Y$ 에 미치는 영향을 분석하고 예측한다.

수학적 모델

다중 회귀 모델은 다음과 같은 수학적 형태를 가진다: $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \epsilon$ 여기서,

$y$ : 종속 변수 (예측하고자 하는 값)
$x_1, x_2, \ldots, x_p$ : 독립 변수들 (설명 변수들)
$\beta_0$ : 절편 (회귀선이 y축과 만나는 점)
$\beta_1, \beta_2, \ldots, \beta_p$ : 독립 변수들의 계수 (각 독립 변수가 종속 변수에 미치는 영향력)
$\epsilon$ : 오차 항 (모델이 설명하지 못하는 부분)

목적

다중 회귀의 목표는 주어진 독립 변수들로부터 종속 변수를 가장 잘 예측할 수 있는 계수 $\beta$ 들을 찾는 것이다. 이를 위해 최소 제곱법(Ordinary Least Squares, OLS)을 사용하여 다음 목적 함수를 최소화한다: $\min_{\beta_0, \beta_1, \ldots, \beta_p} \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip}))^2$

가정

선형성: 독립 변수와 종속 변수 사이의 관계가 선형이어야 한다.
독립성: 관측치 간의 오차가 독립적이어야 한다.
등분산성: 모든 관측치의 오차 분산이 동일해야 한다.
정규성: 오차 항이 정규 분포를 따라야 한다.
다중 공선성: 독립 변수들 간에 강한 상관관계가 없어야 한다. 다중 공선성 문제는 독립 변수들 간의 상관관계가 매우 높은 경우를 의미한다. 이를 확인하기 위해 분산 팽창 계수(Variance Inflation Factor, VIF)를 사용한다.

예제

예를 들어, 주택 가격을 예측하기 위해 방의 개수, 집의 크기, 위치 등의 독립 변수를 사용할 수 있다. 이를 통해 주택 가격에 영향을 미치는 여러 요인들을 분석하고 예측할 수 있다.

구현

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 샘플 데이터 생성
# X는 방의 개수와 집의 크기를 의미한다 (두 개의 독립 변수)
X = np.array([[1, 800], [2, 1200], [3, 1500], [4, 1800], [5, 2000]])
y = np.array([300, 400, 500, 600, 700])  # 주택 가격 (종속 변수)

# 학습 데이터와 테스트 데이터로 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 생성 및 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')

# 회귀 계수
print('Coefficients:', model.coef_)
print('Intercept:', model.intercept_)

입력층(Input Layer): 입력 데이터를 받습니다.
은닉층(Hidden Layer): 입력 데이터의 패턴을 학습한다. 은닉층은 여러 개일 수 있다.
출력층(Output Layer): 예측값을 출력한다.

학습 과정

신경망 회귀 모델은 다음 과정을 통해 학습됩니다:

순전파(Forward Propagation): 입력 데이터가 네트워크를 통과하며 각 뉴런에서 활성화 함수를 거쳐 출력을 생성한다.
손실 계산(Loss Calculation): 예측값과 실제값 사이의 차이를 손실 함수(loss function)를 통해 계산한다. 회귀 문제에서는 주로 평균 제곱 오차(Mean Squared Error, MSE)가 사용된다.
역전파(Backward Propagation): 손실을 최소화하기 위해 가중치와 편향을 업데이트한다. 이를 위해 경사 하강법(Gradient Descent)과 같은 최적화 알고리즘을 사용한다.
반복(Iteration): 위 과정을 여러 번 반복하여 모델의 가중치와 편향을 최적화한다.

활성화 함수

각 뉴런의 출력은 활성화 함수(activation function)를 거쳐 계산된다. 회귀 문제에서는 주로 ReLU(Rectified Linear Unit)와 같은 활성화 함수를 사용한다.

구현

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 샘플 데이터 생성
X = np.array([1, 2, 3, 4, 5])
y = np.array([1.2, 1.9, 3.1, 3.9, 5.1])

# 신경망 모델 생성
model = Sequential()
model.add(Dense(10, input_dim=1, activation='relu'))  # 은닉층
model.add(Dense(1))  # 출력층

# 모델 컴파일
model.compile(optimizer='adam', loss='mean_squared_error')

# 모델 학습
model.fit(X, y, epochs=100, verbose=0)

# 예측
y_pred = model.predict(X)

# 시각화
plt.scatter(X, y, color='blue')  # 데이터 포인트
plt.plot(X, y_pred, color='red')  # 예측선
plt.xlabel('X (광고비)')
plt.ylabel('y (매출)')
plt.title('신경망 회귀 예제')
plt.show()

Linear Layer vs 2 Layers Neural Network

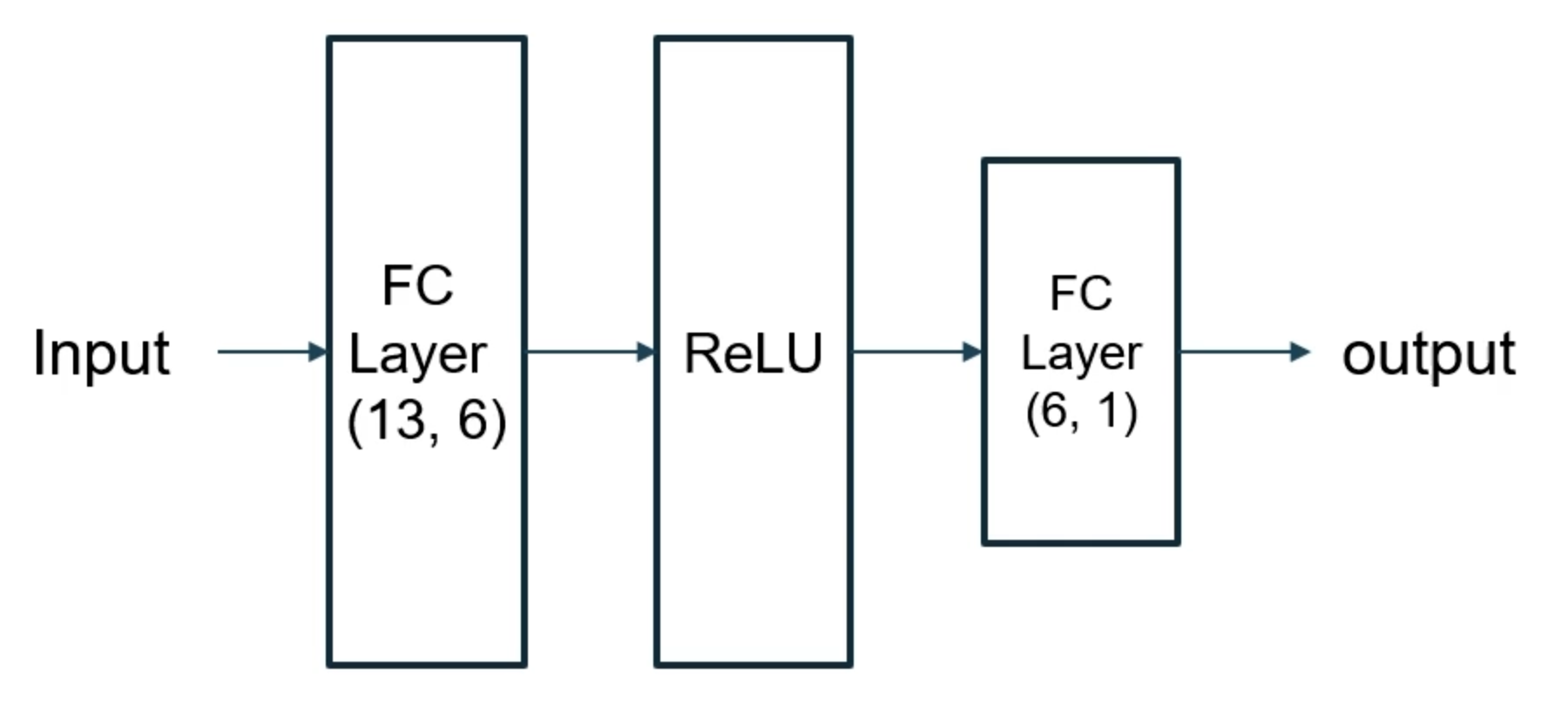
2 Depth Fully Connected Layer

1. 입력을 13으로 가정
1. 첫번째 FC 레이어의 Input demension은 13이고 Output demension은 그의 절반 정도인 6으로 지정
1. ReLU 통과
1. 두번째 FC 레이어의 Input demension은 6이고 Output demension은 1

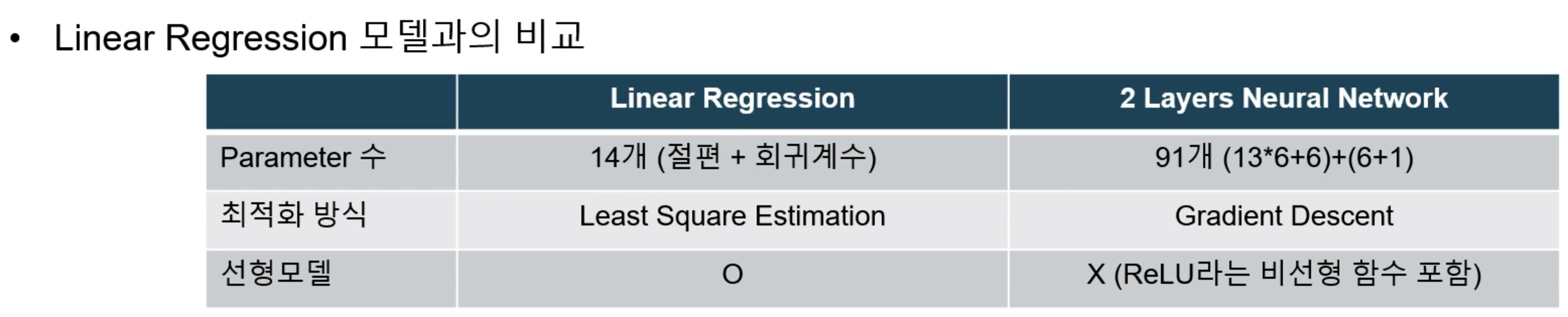
비교

이런 분들께 추천한다!

딥러닝에 흥미가 있지만 시작이 어려우신 분
Pytorch 기본기를 탄탄히 하고 싶으신 분
실습 경험을 쌓고싶은 취준생, 대학생, 비전공자

서포터즈 강의료 지원을 받아 작성하였습니다

[메타코드 강의 후기] 딥러닝 Deep Learning | Regression

One-Hot Encoding

예제

구현

Regression

Linear Regression

정의

수학적 모델

목적

가정

예제

구현

Multiple Regression

정의

수학적 모델

목적

가정

예제

구현

Neural Network Regression

정의

구조

학습 과정

활성화 함수

구현

Linear Layer vs 2 Layers Neural Network

2 Depth Fully Connected Layer

비교